10 Find the extreme values of f(x,y) = 2x2 3y2 −4x−5 on the region D = {(x,y) x2 y2 ≤ 16} Solution We first need to find the critical points These occur when f x = 4x−4 = 0, f y = 6y = 0 so the only critical point of f is (1,0) and it lies in the region x2 y2 ≤ 16 On the circle x 2y = 16, we have y2 = 16−x2 and g(x) = f(x,Jacobian Function linksIf uv=e^cosy & uv=e^xsiny find the Jacobian function https//youtube/8D9QGYyUC9IIf u=e^ucosv, y=e^usinv Prove that JJ' = 1 hJacobian Function linksIf uv=e^cosy & uv=e^xsiny find the Jacobian function https//youtube/8D9QGYyUC9IIf u=e^ucosv, y=e^usinv Prove that JJ' = 1 h
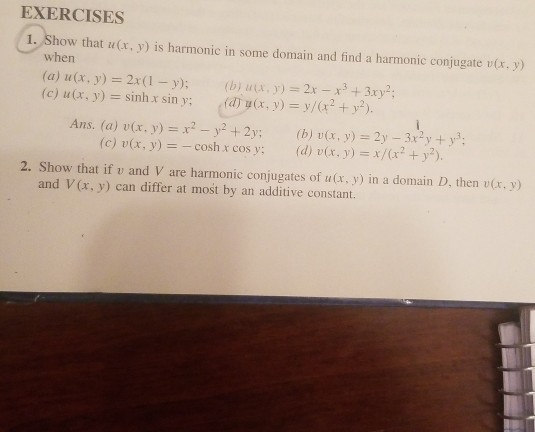
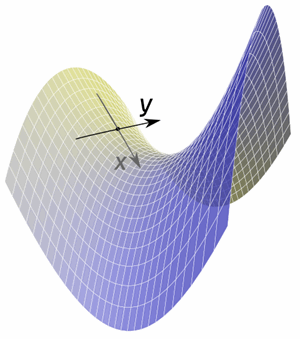
Exercises 1 Show That X Y Is Harmonic In Some Chegg Com
If u(x y)=x^2 y^2 2x-3xy then
If u(x y)=x^2 y^2 2x-3xy then-NCERT Solutions For Class 12 Biology;51 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well



2
If (x y )sin u = x2y2, then x ( partial u/ partial x) y ( Q If (x y )sin u = x 2 y 2, then x ∂ u ∂ x y ∂ u ∂ y =Concept A function f(x, y) is said to be homogeneous of degree n in x and y, it can be written in the form f(λx, λy) = λ n f(x, y) Euler's theorem If f(x, y) is a homogeneous function of degree n in x and y and has continuous first and secondorder partial derivatives, thenIf u = ex^2y^2, then Login Study Materials NCERT Solutions NCERT Solutions For Class 12 NCERT Solutions For Class 12 Physics;
Dx = " 3x2 2 − x3 2 # 1 x=0 = 1 Note that Methods 1 and 2 give the same answer If they don't it means something is wrong 011 Example Evaluate ZZ D (4x2)dA where D is the region enclosed by the curves y = x2 and y = 2x Solution Again we will carry out the integrationNCERT Solutions For Class 12 Chemistry;NCERT Solutions For Class 12 Maths;
33 Rewrite the two fractions into equivalent fractions Two fractions are called equivalent if they have the same numeric value For example 1/2 and 2/4 are equivalent, y/ (y1)2 and (y2y)/ (y1)3 are equivalent as well To calculate equivalent fraction , multiply the Numerator of each fraction, by its respective Multiplier the reqd value, ie, m = x y Then, we have, x = my We submit this x in the given eqn, to get, 2(my) −3y 3(my) −2y = 2 5 ∴ y(2m− 3) y(3m− 2) = 2 5 ∴ 5(2m −3) = 2(3m− 2) ∴ 10m− 15 = 6m −4 ∴ 10m− 6m = ∗ 4m = ∗ 15 −4 = ∗ 11 ∗ ∴ Reqd Value m = 11 4, as before!Let `1/x = u and 1/y = v` Then, equations (1) and (2) become u v = `4/3 and u 2v = 10/3` Adding, We have 9v = 6 ⇒ v = `6/9 = 2/3` ⇒ `1/y = 2/3 ` ⇒ y = `3/2` Substituting y = `3/2` in (1), We have `1/x 2/3 = 4/3` ⇒ `1/x = 6/3 = 2` ⇒ x = `1/2` Hence, x = `1/2 and y = 3/2` Concept Equations Reducible to Linear




Math 300 Problem Set 3 Solutions 1 Using The Cauchy Ubc Math



Http Edshare Soton Ac Uk Id Document 4796
Yu x = xu y (3) yu x xu y = 0 (4) x 2 u y y 2 u x = 0 pre calculous use the properties of logarithms to write the expression as a sum or difference of logarithms or multiples of logarithms show your work ln x^2/y^3 Assuming x,y AND z are positive use properties of logariths to write theSolution The equation is Substitute x=2 in the equation, Therefore, the value of y is 3 So, Option b is correct #Learn more If x=3 and y=4 find x23xyy2 brainlyin/question/



Http Cloudportal Sathyabama Ac In Coursematerial Staging Uploads Smta1105 Pdf



Partial Derivatives
If u=sin1((x^2y^2)/(xy)) then show that x(du/dx)y(du/dy)=tan u MATHEMATICS1 question answer collection1(r)es, x y = 2c 2(r)e s, so x2 y2 = (xy)(x y) = 4c 1(r)c 2(r), ie is a constant along the projected characteristic curves In other words, the projected characteristic curves are x 2 y = C, C a constant, and the solution is a function that is constant along these One has toGiven equation2x2 xy −3y2 xay −10 = (2x3y b)(x−y−2)⇒ 2x2 xy−3y2 xay−10 =2x2 3xybx−2xy−3y2 −by −4x−6y −2b⇒ 2x2 xy−3y2 xay−10 =2x2 xy −3y2 (b−4)x−(b6)y−2bComparing the coefficients of x,y and constants will getb−4 = 1(i)−(b6) = a(ii)−2b = −10(iii)From eq (1), we get⇒ b



Cluster28 Files Instructure Com Courses 1875 376 Files 1875 Course files Homework Homework Solutions S14 V2 Pdf Download Frd 1 Sf Verifier Ts User Id Verifier F6odfk5wtmvwacsbq5zj075bewxeq5c3onwt0euw




Show That The Equation Tex X 2 3xy 2 Y 2 2x 3y 35 0 Tex For Every Real Value Brainly In
And by the symmetry of uin xand y, u yy= 2x2 22y (x2 y2)2 Clearly then u xx u yy= 0 in this case If u= arctan(y=x), then by the chain rule again u x= 1 1 (y x) 2 y x 2 = 2y x y 2) u xx= (x y2)(0) ( y)(2x) (x y2Factor 2x^23xyy^2 2x2 3xy y2 2 x 2 3 x y y 2 For a polynomial of the form ax2 bx c a x 2 b x c, rewrite the middle term as a sum of two terms whose product is a⋅c = 2⋅1 = 2 a ⋅ c = 2 ⋅ 1 = 2 and whose sum is b = 3 b = 3 Tap for more steps Reorder terms 2 x 2 y 2 3 x y 2 x 2 y 2 3 x y Reorder y 2 y 2 and 3Calculus Solve for y x^23xyy^2=1 x2 − 3xy y2 = 1 x 2 3 x y y 2 = 1 Move 1 1 to the left side of the equation by subtracting it from both sides x2 − 3xyy2 − 1 = 0 x 2 3 x y y 2 1 = 0 Use the quadratic formula to find the solutions −b±√b2 −4(ac) 2a b ± b 2 4 ( a c) 2 a Substitute the values a = 1 a = 1, b



How To Solve The Differential Equation 2y 3xy 2 Dx X 2x 2y Dy 0 Quora



Www Stewartcalculus Com Data Essential calculus 2e Upfiles Instructor Eclt Ax 1103 Pdf
Mumbai University > First Year Engineering > Sem 1 > Applied Maths 1 Marks 6 M Year May 15U = x /y x = uy dx/dy = u for a full explanation x= uy xvx = u(yvy) where v is a tiny fraction ( I can't do the delta symbol) xvx = uyuvy xvx x = uyuvy uy vx = uvy vx/vy = u Limit as v > 0, dx/dy = u Use the power rule, dy/dx = nx^ (x1) d y d x = n x x − 1 , on the first term 2x (3d (xy))/dx (d (y^2))/dx= (d (0))/dx 2 x 3 d ( x y) d x d ( y 2) d x = d ( 0) d x Use the product rule, (d (xy))/dx= dx/dxyxdy/dx = y xdy/dx d ( x y) d x = d x d x y x d y d x = y x d y d x




Multivariate Functions And Partial Derivatives Sage Research Methods




Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy
If x^2 xyy^3 = 0, then, in terms of x and y, dy/dx = 2x y/x 3y^2 x 3y^2/2x y 2x/1 3y^2 2x/x 3y^2 2x y/x 3y^2 1 Get more help from Chegg Solve it with our calculus problem solver and calculatorR x as boundaries the curves x2 −y2 = 1, x2 −y2 = 4, y = 0, y = x/2 Solution Since the boundaries of the region are contour curves of x2 −y2 and y/x , and the integrand is y/x, this suggests making the change of variable (23) u = x 2 −y 2 , v = y x We will try to get through without solving these backwards for x, y in terms of u, vAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction yx^ {2}y^ {2}xu=0 y x 2 y 2 x − u = 0 This equation is




If Math 3x 4y Sqrt Xy Math How Can You Prove That Math X 2 Y 2 Xy Math Quora



Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is A Parameter From Class
Mathx=s3t/math math\frac{d}{ds}x^2=\frac{d}{ds}(s3t)^2/math math=2(s3t)/math math\frac{d^2}{ds^2}x^2=\frac{d}{ds}(\frac{d}{ds}x^2)/math math Consider the family of circles x^2y^22x2lambda8=0 passing through two fixed points n dB Then the distance between the points n dB is_____ This browser does not support the video element 31 k 18 k Answer Step by step solution by experts to help you in doubt clearance & scoring excellent marks in examsQuestion if x=1 and y=2 what is the value of expression 2x^3 3xy Answer by Alan3354() ( Show Source ) You can put this solution on YOUR website!



If X Y 2 Then What Is The Value Of X Y 6xy Quora




Solving A System Of Equations Using A Matrix Precalculus Socratic
Answer to Given u = x^2 y^2, v = xy , find the Jacobian \\frac{\\partial(x,y)}{\\partial(u,v)} By signing up, you'll get thousands ofIf u(x, y) = 2x2 − 2y2 4xy is a harmonic function, then its conjugate harmonic function v(x, y) is Q7 f(z) = u(x, y) iv(x, y) is an analytic function of complex variable z = x iy$\endgroup$ – mir (x,y) x^{2}y^{2} \leq a^{2}\}$ in the first quadrant Hence the limts are $0
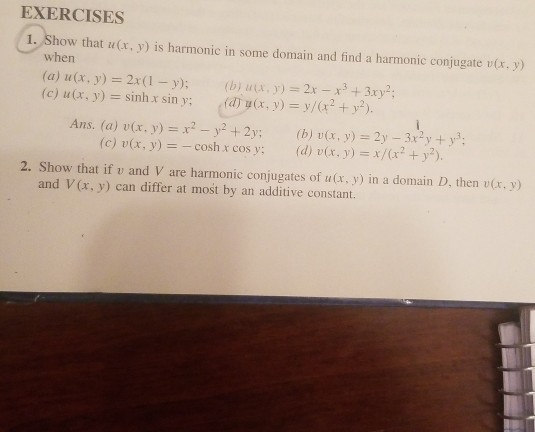



Exercises 1 Show That X Y Is Harmonic In Some Chegg Com



Www3 Nd Edu Taylor Math550 Images Worksheets Solutions05 Pdf
of pretzels Each bag contains 7 servings, She is planning to have 30 guests at her party To determine how many bags she needs to buy, she sets up an inequality and solves it tex7x\geq 30\\x\geq 43/tex She determines that she needs to buy at least 4 bags of pretzels to ensure that anyone has at least one serving1 A harmonic function is analytic if it satisfies the Laplace equation If 𝑢(𝑥,𝑦) = 2𝑥2 −2𝑦2 4𝑥𝑦 is a harmonic function, then its conjugate harmonic function 𝑣(𝑥,𝑦) is (A) 4𝑥𝑦 −2𝑥2 2𝑦2 constant (B) 4𝑦2 −4𝑥𝑦 constant 2𝑥2 −2𝑦2 𝑥𝑦 constant (D) −4𝑥𝑦 2𝑦2 −2𝑥2 constant Discuss below to share your Correction (after missing a sign) As kobe pointed out, the original DE is $$ (x^2y^2)y'2xy=0, $$ which as equation for a vector field reads $$ (x^2y^2)\,dy2xy\,dx=0\iff Im(\bar z^2\,dz)=0\text{ with } z=xiy $$ From the complex interpretation it is directly visible that this is not integrable, for that it would have to be an expression




Implicit Differentiation Advanced Example Video Khan Academy



Http Wwwf Imperial Ac Uk Eskelton Partialdiff Pdf
If V = z e a x b y and z is a homogeneous function of degree n in x and y, prove that x ∂ x ∂ V y ∂ y ∂ V = (a x b y n) V View solution View moreSuppose f(x,y)=3/(x^2y^2)and u is the unit vector in the direction of 〈1,2〉 Then, (a) ∇f(x,y)= (b) ∇f(2,2)= (c) fu(2,2)=Duf(2,2)= $$\int_{0}^a\int_{0}^\sqrt{a^2y^2} (2x3xy)\,dx\,dy$$ In this question I want to solve it by using polar $\begingroup$ That's i know but in some cases other than circle i have to do more complex substitutions then how will i determine?




Differentiate X 2 Y 2 3xy 1 Youtube




Ex 5 3 6 Find Dy Dx In X3 X2y Xy2 Y3 81 Cbse
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method xy=2;2x3y=2 Tiger Algebra SolverStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeIntegrating Factors Some equations that are not exact may be multiplied by some factor, a function u (x, y), to make them exact When this function u (x, y) exists it is called an integrating factor It will make valid the following expression ∂ (u·N (x, y)) ∂x = ∂ (u·M (x, y)) ∂y




Verify That The Differential Equation 3xy Y 2 Chegg Com




If 2x 2 3xy Y 2 X 2y 8 0 Then Dy Dx Youtube
X3yx2y2xy=0 Four solutions were found x = 2 x = 1 y = 0 x = 0 Step by step solution Step 1 Step 2 Pulling out like terms 21 Pull out like factors x3y x2y Consider x^ {2}2xy3y^ {2} as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and mIf u = x 2 − y 2, v = 2 x y a n d z = f ( u, v) prove the following written 50 years ago by shailymishra30 ♦ 330 modified 14 months ago by sanketshingote ♦ 570 ( ∂ z ∂ x) 2 ( ∂ z ∂ y) 2 = 4 u 2 v 2 ( ∂ z ∂ u) 2 ( ∂ z ∂ v) 2 partial differentiation ADD COMMENT Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by




If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx
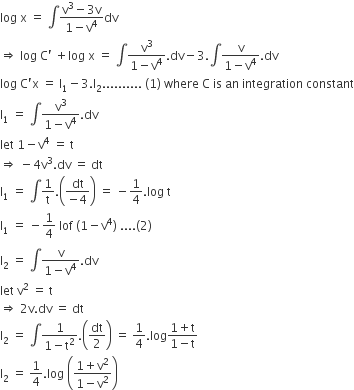



Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is A Parameter From Class
Calculus Find dy/dx x2xyy^2=2 x 2xy y2 = 2 x 2 x y − y 2 = 2 Differentiate both sides of the equation d dx (x 2xy y2) = d dx(2) d d x ( x 2 x y − y 2) = d d x ( 2) Differentiate the left side of the equation Tap for more steps If #u= (12xyy^2)^1/2# , then show that #x(partial u)/(partial x)y(partial u)/(partial y)= y^2u^3# ?If u= log(x2 y2), then by the chain rule u x= 2x x 2 y) u xx= (x2 y2)(2) (2x)(2x) (x 2 y) = 2y2 2x2 (x y2)2;




Doc Partial Derivative Mcq S Assignement Innocentboy Nishant Academia Edu




Solved 4 6 Find The Directional Derivative Of F A
If Var (x) = 5, Var (y) = 3396 and Cov (x, y) = 102, then the correlation coefficient is If Vectors A 2i J K B I 2j 3k C 3i Lambdaj 5k Are Coplanar Then The Value Of Lambda Is Equal To If W Is One Cube Root Of Unity Then Find The Determinant Given If x = 2 and To find The value of y ?Y2 2 # y=x y=0 dx = Z 1 0 3x−x2 − x2 2!




Partial Differentiation
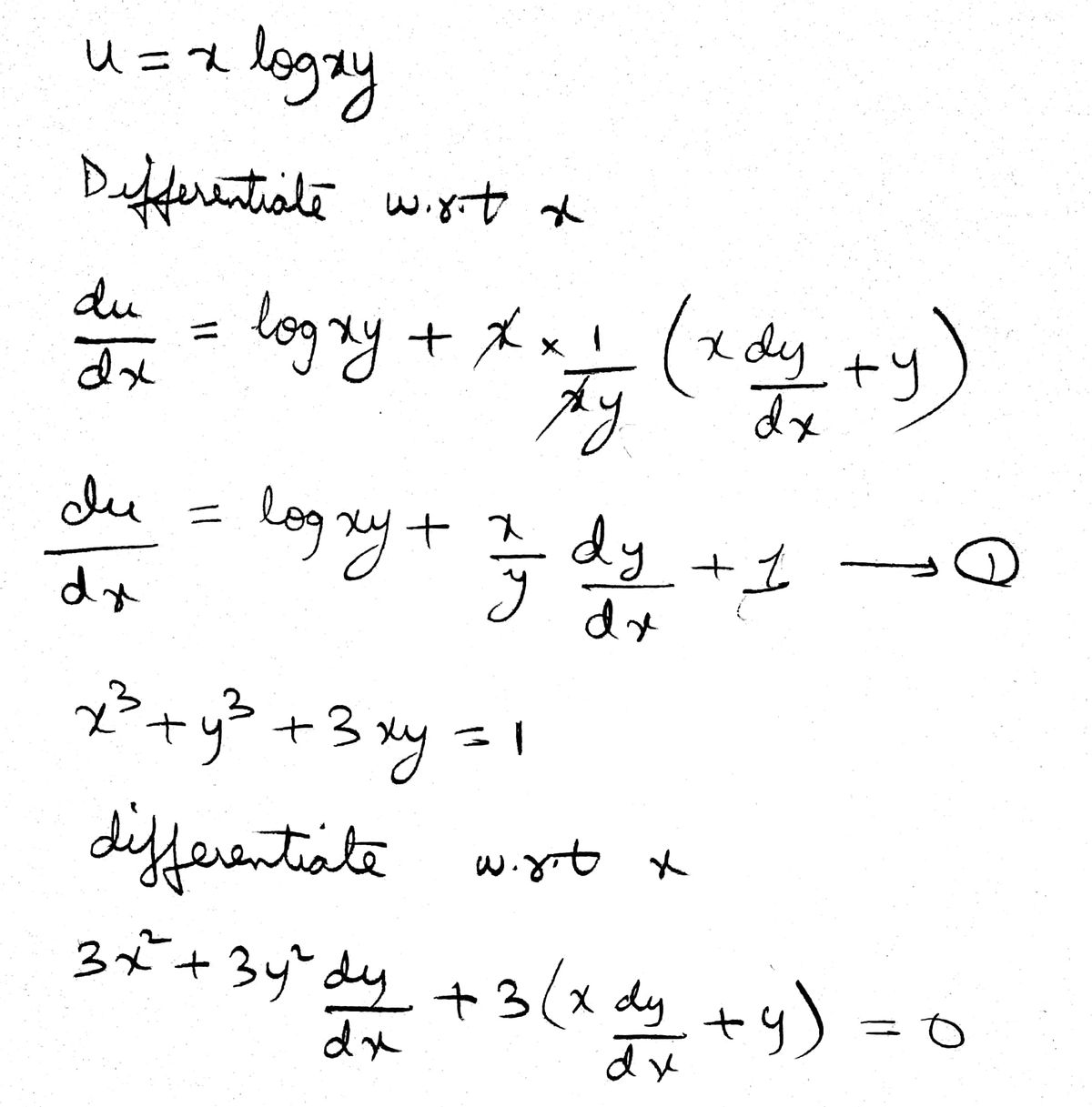



Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby
If u = log(x^2 y^2)/xy then x(∂u/∂x) y(∂u/∂y) is (a) 0 (b) u (c) 2u asked in Differentials and Partial Derivatives by RamanKumar ( 499k points) If, (xy/xy) = u/v then, show this (x^2 xy/xyy^2) = (u^2 uv/uvv^2) In a class, the ratio of the number of students having height below 4 ft to the ones having height equal to4 ft is 35Dx = Z 1 0 3x− 3x2 2!




If X 2 Y 2 3xy 0 And X Gt Y Then Find The Value Of Log
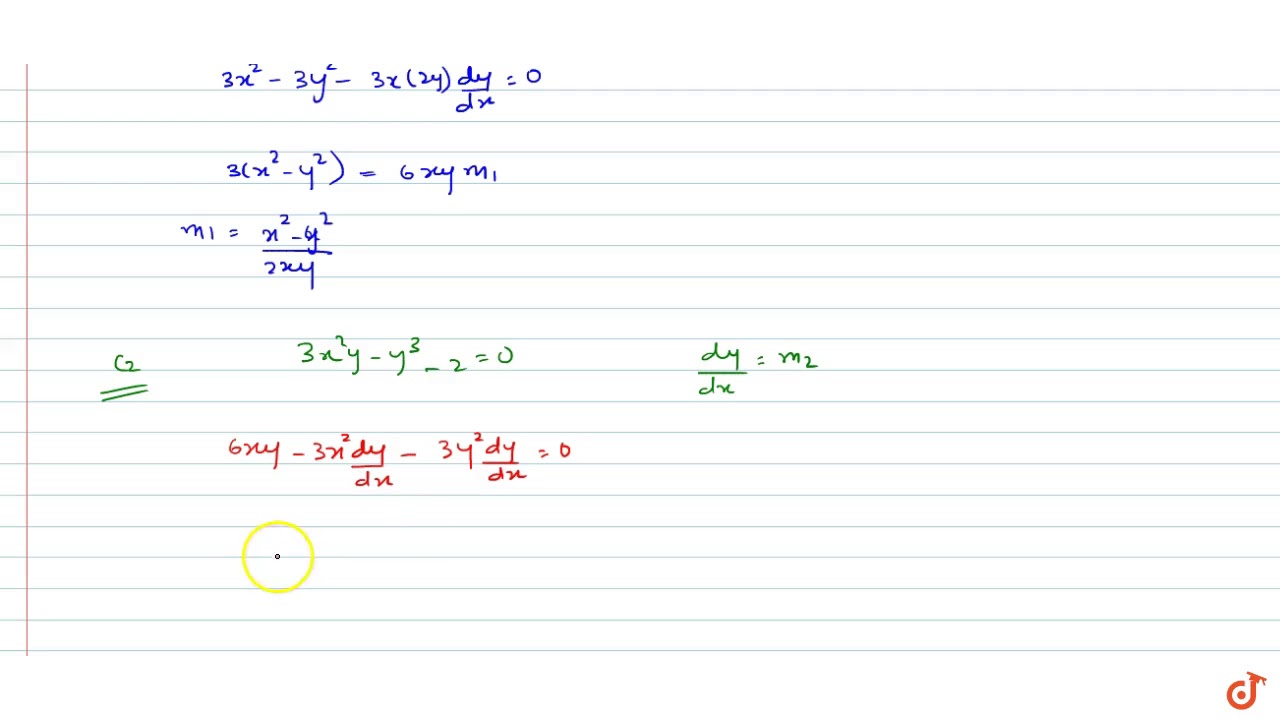



The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube
The given information is u = log(x2 y2x4 y4 )Taking partial differentiation wrt to x and y one at a time we get,⇒ ∂ x∂ u = x4 y4x2 y2 (x2 y2)24x3(x2 y2)−2x(x4 y4) ⇒ ∂ x∂ u = (x4 y4)(x2 y2)4x5 4x3y2 −2x5 −2xy4 ⇒ ∂ y∂ u = x4 y4x2 y2 (x2 y2)24y3(x2 y2)−2y(x4 y4) ⇒ ∂ y∂ u = (x4 y4)(x2 y2)4y5Jacobian Function linksIf uv=e^cosy & uv=e^xsiny find the Jacobian function https//youtube/8D9QGYyUC9IIf u=e^ucosv, y=e^usinv Prove that JJ' = 1 h




If X Y 7 And X 3 Y 3 133 Find X 2 Y 2 Brainly In



Www Tau Ac Il Levant Ode Solution 6 Pdf




Partial Derivative Examples Math Insight
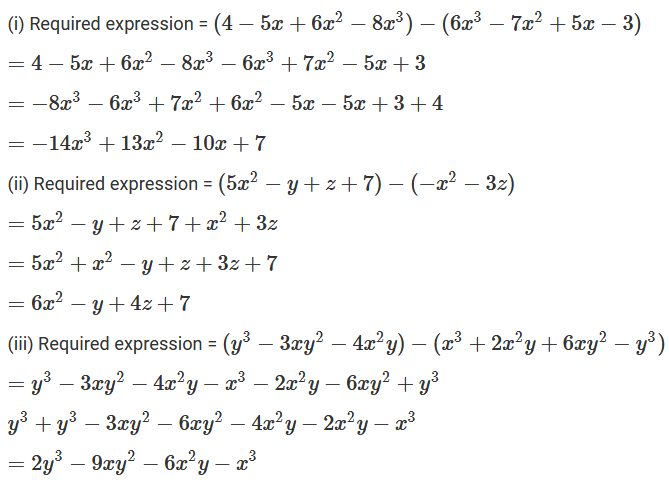



R D Sharma Solutions Class 7 Math Chapter 7 Algebraic Expressions Exercise 7 2
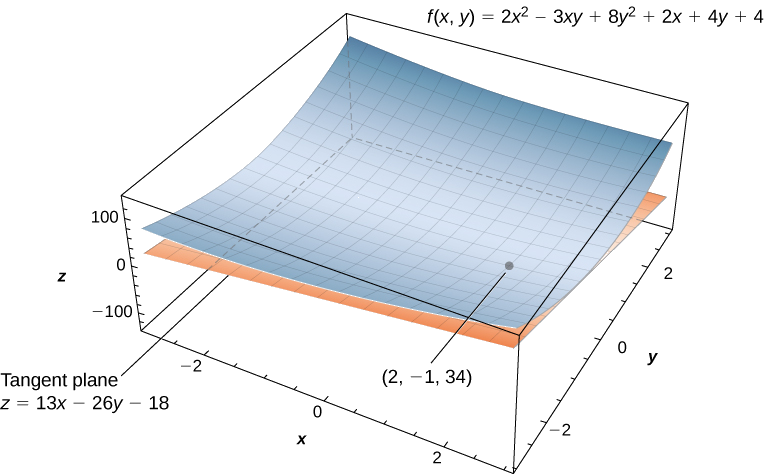



14 4 Tangent Planes And Linear Approximations Mathematics Libretexts




If U F R Where R 2 X 2 Y 2 Then 2u X 2 2u Y 2




When X 2 Y 2 T 1 T And X 4 Y 4 T 2 1 T 2 Then How Do You Prove That Dy Dx 1 X 3y How Would You Solve This Quora




X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube



Http Maths Dur Ac Uk Users Daniel Evans Mes Messolutionsupdated Pdf



1



2
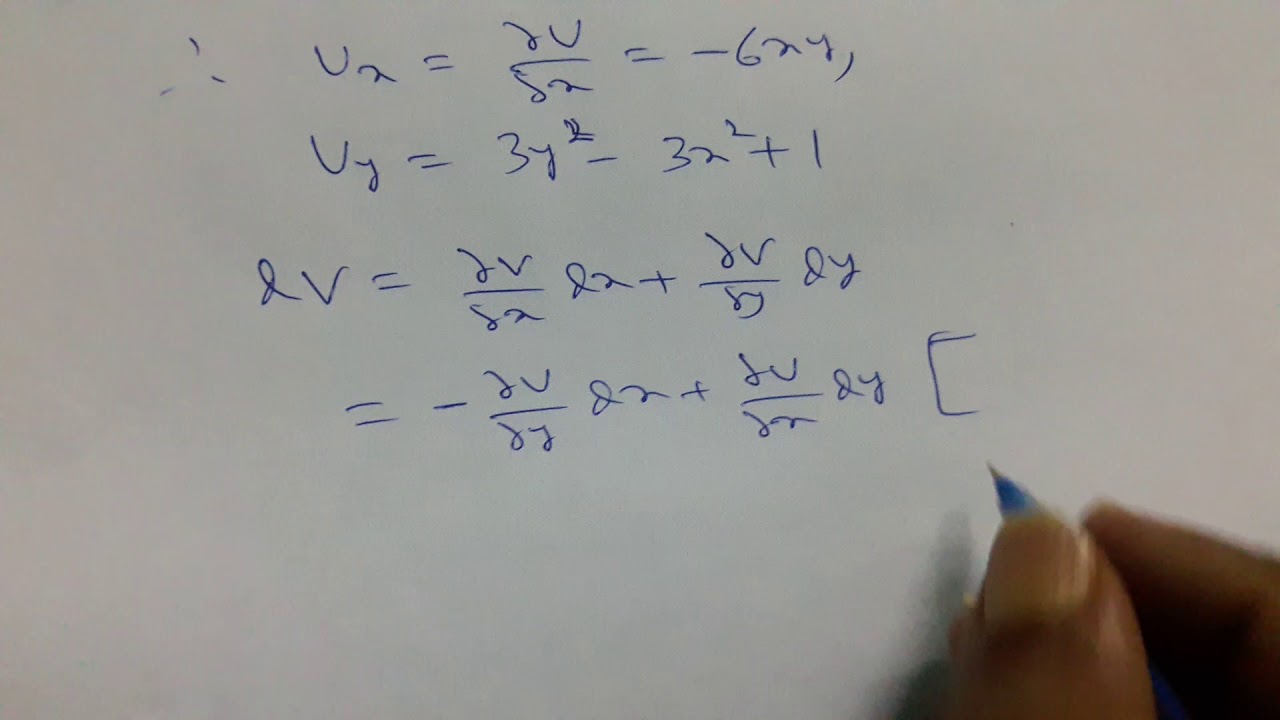



If U X Y Y 3 3x 2 Y Y Determine V X Y So That F U Iv Is An Analytic Function Youtube




F X Y 2x 2 3xy 4y 2 Find Y If F 3 Y 3 Sat Act Multiple Choice Youtube



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com



If Math X Y 2 Text And X 2 Y 2 2 Math What Is The Value Of Math Xy Math Could You Break It Down For Me Quora




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




If X 2 Y 2 3xy Then Choose The Correct Answer Of 2log X




If 4x 2 Xy 3xy Y 2 12 5 Find X 2y 2x Y Brainly In



If U X Y Z Xy 2z 3 X Sin T Y Cos T Z 1 E 2t Find Du Dt Sarthaks Econnect Largest Online Education Community



Q Tbn And9gcqarbprtbhwliutl2bsbxh5h Cag9wmmdvwdb4top Bjd8i W T Usqp Cau




Use Partial Derivatives To Find Dy Dx If Y F X Is Chegg Com
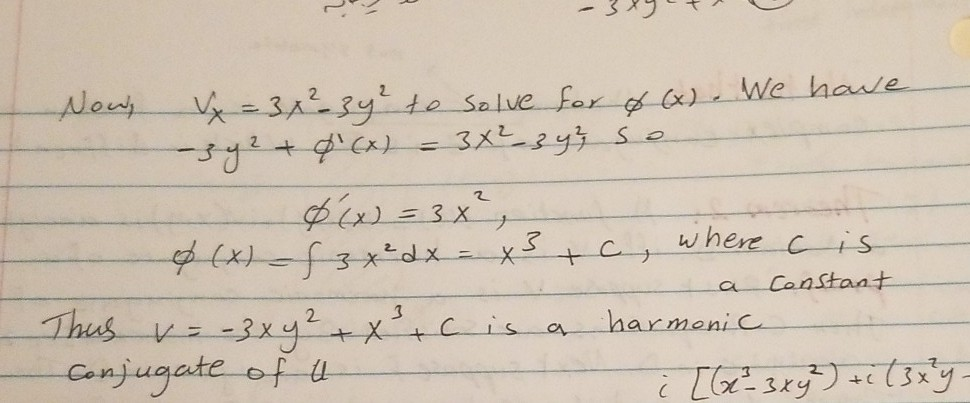



Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com




Solutions To Implicit Differentiation Problems



2



Q Tbn And9gctuowuwpwgabmsscw7hciwf8vtunjxc8g8hfqj5uaw Usqp Cau




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Find The Critical Points Of The Following Functions Use The Second Derivative Test To Determine If Possible Whether Each Critical Point Corresponds To A Local Maximum Local Minimum Or Saddle Point Confirm
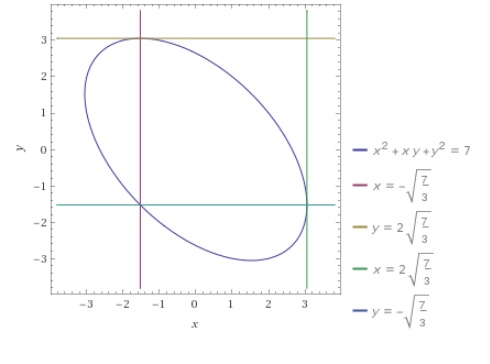



How Do You Find All Points On The Curve X 2 Xy Y 2 7 Where The Tangent Line Is Parallel To The X Axis And The Point Where The Tangent Line




Chapter 1 Partial Differential Equations Ppt Video Online Download



3 8 Implicit Differentiation Calculus Volume 1




R D Sharma Solutions Class 7 Math Chapter 7 Algebraic Expressions Exercise 7 2




Partial Differentiation



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus2 Pagine Lineintex Pdf




Chapter 7 Calculus Of Several Variables




If 2x 2 3xy Y 2 X 2y 8 0 Then Dy Dx



2



Http Www2 Imperial Ac Uk Jdg Ae6soln Pdf



Www Ualberta Ca Rjia Math215 Hwks Sol8 Pdf




Jacobians New
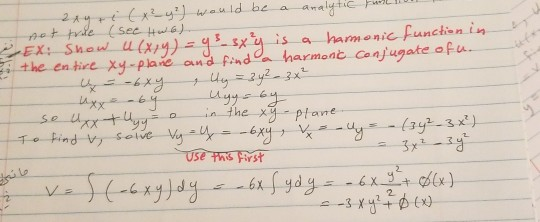



Exercises 1 Show That U X Y Is Harmonic In Some Chegg Com



Find An Analytic Function Whose Real Part Is U X 3 3xy 2 3x 2 3y 2 3y 2 1 Sarthaks Econnect Largest Online Education Community




If X 2 And X Square Y Square 3xy 5 Then Find Y Brainly In




University Calculus Elements With Early Transcendentals 1st Edition H




Solve Each System Use Any Method You Wish 2x 2 Chegg Com




Solve The Equation X 2 3xy Y 2 Dx X 2dy 0 Given That Y 0 And X 1




11 Business Math Stats Vol 2 Em Pages 51 100 Flip Pdf Download Fliphtml5




T Qmo3 If Uleft X1yright 4x Y See How To Solve It At Qanda
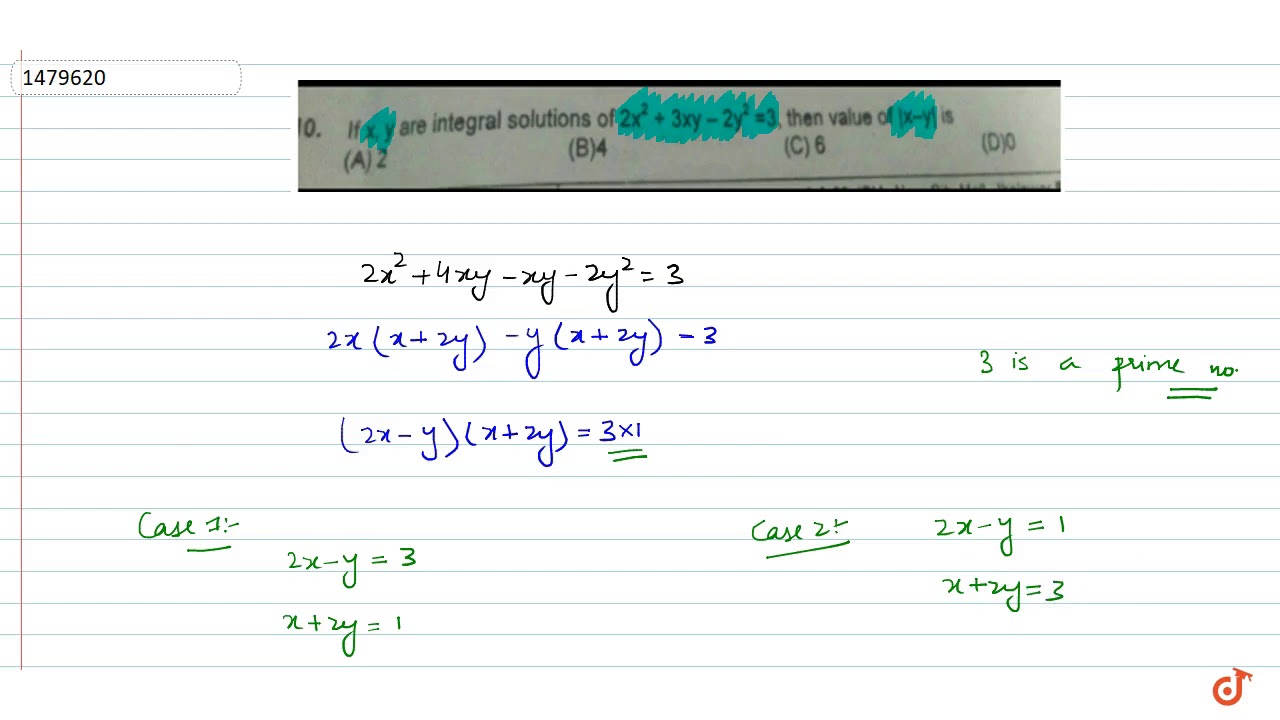



If X Y Are Integral Solutions Of 2x 2 3xy 2y 2 3 Then Value Of X Y Is Youtube




Assignment No



2




If X 3 2x 2y 2 5x Y 5 0 And Y 1 1 Then A Y Prime 1 4




Answered Find All The Second Order Partial Bartleby



1



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




2 Partial Differentiation




Vector Analysis By Alimkanwalimtinaa Issuu




If X Y Are Integral Solutions Of 2x 2 3xy 2y 2 7 Then



If U X 2tan 1 Y X Y 2tan 1 X Y Prove That 2u Y X X 2 Y 2 X 2 Y 2 Sarthaks Econnect Largest Online Education Community




T Qmo3 If Uleft X1yright 4x Y See How To Solve It At Qanda



Calculus Part 3 Early Transcendentals 8th Edition 15 Pages 1001 1404 Flip Ebook Pages 1 50 Anyflip Anyflip



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf



Http People Whitman Edu Hundledr Courses M125f04 Examrev2sol Pdf



Cnx Org Exports F10a2a32 9eca 48cf 9e84 10c18a0484 403 Pdf The Chain Rule 3 Pdf



2




Pplato Basic Mathematics Gradients And Directional Derivatives



2




Pdf On The Diophantine Equation X2 Kxy Y2 2n 0




Find Dydx Where X 2 Y 2 3xy 1




Analytic Functions Mcq Notes Equations Functions And Mappings


